Today, most spatial databases know how to deal with a round earth. For example, they can tell you the distance between New York and London, or find the area within 1000 km of a point — tasks not normally possible with a flat map. So, I thought it would be interesting to explore a few spatial operations with three of the major databases: SQL Server 2012, Oracle 11g R2, and PostGIS 2.0. (DB2 and Informix also have round-earth extensions, but I won’t cover them here.)
I was focused on two questions:
- Do they all produce essentially the same output? (This gives me confidence about their quality without having to independently determine the “right” answers.)
- As noted previously, only SQL Server models round-earth curves. Is that a benefit?
Experiment 1:
How far is it from Vancouver, Canada to Tokyo, Japan?
I loaded a two-point round-earth line into each system and asked for its length. Here are the (uncontroversial) results:
| Oracle | 7572654.086m | |
| PostGIS | 7572654.091m | |
| SQL Server | 7572658.675m |
Experiment 2:
What is the shortest path from Vancouver to Tokyo?
Here, I’m interested in getting a densified line which allows for (a) comparison and (b) visualization in round-earth-unaware applications.
This is trickier; in each system the round-earth spatial functions have evolved from flat-map ones, and it doesn’t make sense to densify a line on a flat map, so there isn’t a call to do it. My first attempt was to intersect the Vancouver-Tokyo line with a large number of north/south lines and plot the intersection points. This worked well for Oracle and SQL Server, but less so for PostGIS:
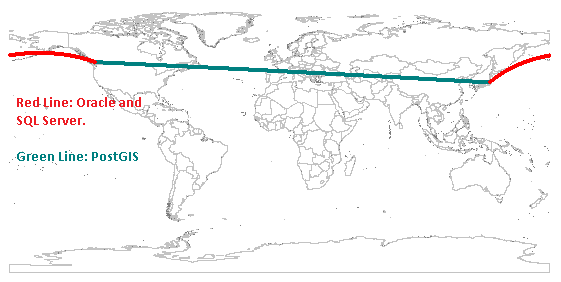
Motivated to find an answer, I tried an approximation: Cover the earth with a grid at 1×1 degree intervals, find the distance between each point and the line, keep the ones within 200 km, and buffer these together. This produced a consistent result:
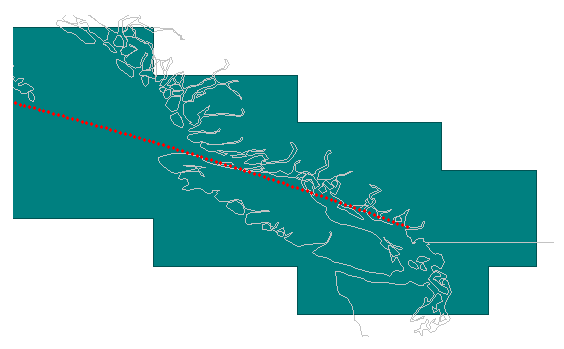
Experiment 3:
What area is within 1 km of the shortest path from Vancouver to Tokyo?
I asked each database to buffer the line (from Experiments 1 and 2) by 1 km. Only SQL Server produced the correct result; both Oracle and PostGIS followed the path PostGIS took in Figure 1.
Further, if I used SQL Server’s BufferWithCurves() method, it was able to produce a compact result consisting of five arcs.
Experiment 4:
What area is within 100 km of Vancouver’s airport?
I asked each database to buffer a point representing the airport by 10, 100, and 1000 km. The answers in each case were consistent and reasonable.
The majority of the differences between the three database’s answers came down to the density of the output (i.e., how many vertices made up the boundary). Oracle returned more vertices when the tolerance value was decreased (as expected), SQL Server appeared to ignore the tolerance value (unless I buffered as arcs, and then used CurveToLineWithTolerance), and PostGIS didn’t provide an option.
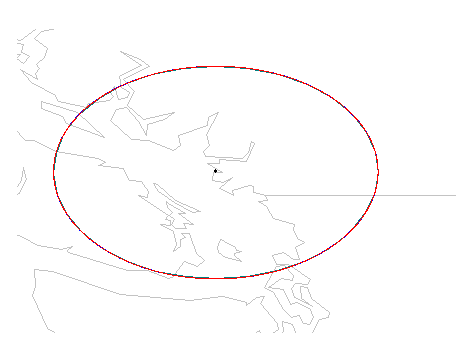
Experiment 5:
Are there any surprises when using round-earth curves for small objects?
The previous examples demonstrate SQL Server’s ability to use round-earth arcs to represent large areas on the earth (e.g., 100 km around an airport, 1 km around a flight path). Given that SQL Server’s round-earth arc representation is new, it makes sense to ask if it behaves intuitively for small objects.
I digitized a cul-de-sac near the Safe Software office using three-point arcs. Then I wrote the resulting (curve) polygon to SQL Server. I also wrote a stroked version of the polygon (replacing the curved segments with shorter straight lines) to Oracle, PostGIS, and (again) SQL Server. To test that the curved polygon behaved similarly to its stroked equivalent, I asked each database for the polygon’s area:
| Oracle (stroked polygon) | 1615.100 m2 | |
| PostGIS (stroked polygon) | 1615.100 m2 | |
| SQL Server (curved polygon) | 1614.938 m2 | |
| SQL Server (stroked polygon) | 1615.100 m2 |
This suggests curved data may be loaded into round-earth columns and processed normally.
Conclusion
Returning to my two opening questions:
> Do they all produce essentially the same output?
Yes. These databases generally return consistent results for round-earth queries. There are minor variations, and not everything works in all cases, so care is required.
> Only SQL Server models round-earth curves. Is that a benefit?
Yes. SQL Server’s round-earth curves allow geometry to be stored more compactly without loss of detail. Perhaps more importantly, curved data can be loaded into round-earth columns without degrading the data (i.e., by converting the curves into lines).
During this exercise, I noticed an error in my previous post. I had thought SQL Server had introduced the buffering-with-curves idea. Not so: For example, Oracle has had this ability for flat-map buffering for a very long time.
Spatial databases can efficiently and effectively store, query, and transform data, all while honoring the curvature of our round world. How are you taking advantage of these capabilities?
Paul Nalos
There should be a better way to make a “renderable” version of the great circle paths than either of the hacks you had to do. I’ve been meaning to extend ST_Segmentize() to handle the geography type, and I think you just pushed me over the edge to go and do that. Then your PostGIS query to generate a renderable great circle would be
SELECT ST_Segmentize(ST_MakePoint(, )::geography);
Thanks Paul! I didn’t know about ST_Segmentize(); to the extent my use case is real, this will be a great addition to PostGIS (and a first, I think, for the three databases compared here).
I did a quick test to see if that would be enough to improve the “buffer long line” case (i.e., densify and then buffer) and it seems the answer is no (I get a very interesting donut back), but the improvement is welcome nonetheless.
Hi Paul,
Great post… Can you post the exact start and end LatLng coordinates for Vancouver and Tokyo?
Wouldn’t mind testing a few calculations I use for similar distance checks.
Cheers,
Brendan
Hi Brendan,
I’d be happy to. I used values I found using Google Earth:
In (longitude, latitude) decimal degrees, east positive:
Vancouver: (-123.113927, 49.261226)
Tokyo: (139.691706, 35.689488)
Regards,
Paul
Is “curved polygon”(1614.938 m2) having more area than “stroked polygon”(1615.100 m2) for the convex shape a rounding issue?
Meant to say “less area” not “more area”.
OK, great circle segmentize added to PostGIS for release at version 2.1
select st_astext(st_segmentize('LINESTRING(0 20, 5 20)'::geography, 100000));LINESTRING(0 20,0.832745573421944 20.0097394480269,1.66619627955163 20.0155899605711,2.5 20.017541273713,3.33380372044837 20.0155899605711,4.16725442657806 20.0097394480269,5 20)@Paul: Sounds great. I’m not quite curious enough to build PostGIS from source, but I’ll certainly check it out when the release ships.
@Bala: It’s not so much a rounding issue as an approximation issue. My stroked version of the area is an approximation of the curved area. It’s an approximation in two ways: (i) only twenty-ish coordinates were used to replace each curved segment, and (ii) the curves were densified without geodetic calculations. For (i), if I increase the number of vertices, all three databases converge at 1615.060 m^2 for the stroked version – which is a bit closer. For (ii), I expected a small difference and was just looking to see the answer was close. This was to validate my assumption that for small areas on the earth, flat-earth and round-earth curves should behave similarly.
Regards,
Paul